La paradoja Banach-Tarski y el infinito
Quizá hayas oído la desconcertante frase de que con los fragmentos de un chícharo es posible reconstruir el sol e incluso el universo completo. Pues la frase expresa la esencia de la “paradoja de Banach-Tarski”, un desconcertante teorema de las matemáticas y la teoría de conjuntos que plantea interesantes reflexiones sobre el alcance de las matemáticas, los resultados contraintuitivos de operar con el infinito, la relación entre análisis y síntesis, lo abstracto y lo concreto, y geometrías fractales.
La paradoja Banach-Tarski demuestra matemáticamente que es posible dividir una esfera sólida en “n” número de partes y reconstruir con dichos fragmentos dos esferas idénticas a la primera, con tan solo rotar y permutar las piezas (es decir sin estirarlas o deformarlas).
Vale la pena señalar que Stefan Banach y Alfred Tarski fueron matemáticos polacos. El primero tenía buenas relaciones con los científicos soviéticos, razón por la cual fue sospechoso bajo el régimen nazi y sobrevivió realizando experimentos con piojos donde él mismo era el donante de sangre para alimentarlos. Muy dañado en su salud murió en 1945 recién terminada la ocupación. Alfred Tarski logró emigrar a Estados Unidos poco antes de la invasión de Hitler pero la mayor parte de sus familiares murieron en campos de concentración.
La paradoja en cuestión es el equivalente de “Hotel de Hilbert” aplicado a los puntos de una esfera. Recordemos que en la paradoja del Hotel de Hilbert es posible alojar a un huésped en un hotel infinito completamente lleno, simplemente solicitando a los ocupantes que se cambien a la habitación que resulta de sumar +1 el número de su habitación (lo cual es posible pues infinito +1 es igual a infinito). El nuevo huésped ocupa la habitación número 1. Pero en este hipotético hotel infinito completamente lleno podrían alojarse también un infinito número de huéspedes, solicitando a los ocupantes que multipliquen por 2 el número de su habitación y ocupen el resultado; los nuevos huéspedes se hospedan en los infinitos números impares que quedaron vacíos (esto es posible porque hay infinitos números pares e impares). Algo similar puede hacerse con infinitos camiones llenos de infinitos huéspedes que solicitaran alojamiento en el hotel, esta vez usando los infinitos números primos para cada uno de los infinitos autobuses y un número par o impar para cada uno de los huéspedes de cada camión, cada huésped de toma el número primo de su autobús y lo eleva al número par o impar que se le asignó, resultando la habitación que debe ocupar. La paradoja demuestra que hay diferentes tipos de infinitos –mayores y menores– y que la noción de infinito rompe el “sano” sentido común.
La esfera es, desde un punto de vista geométrico, equivalente a ese hotel infinito puesto que se puede demostrar que una esfera contiene infinitos puntos. La paradoja Banach Tarski implica descomponer en su totalidad la esfera en infinitos puntos, agrupar dichos puntos por el tipo de rotación en la esfera con la cual se obtuvieron (en sentido horario o antihorario, hacia el eje de las x o y). Como los puntos carecen de dimensión, se pueden realizar determinadas operaciones con ellos sin considerar su volumen. Luego es posible reagrupar –integrar– los puntos en piezas con dimensión determinada y formar con dichas piezas dos esferas idénticas a la original.
Sin violar las reglas de las matemáticas, la geometría euclidiana y la teoría de conjuntos es posible repetir esa operación con las nuevas esferas y obtener infinitas de ellas a partir de una. Este resultado increíble es consecuencia de operar con el infinito y llevar a sus últimas consecuencias el descomponer un cuerpo en puntos sin dimensión.
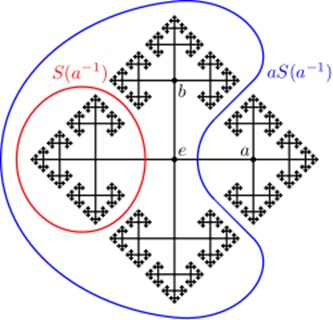
Otra manera de verlo es asignar a cada punto de la esfera otro punto en una estructura geométrica fractal. Los fractales tienen dimensiones irracionales muy extrañas, mayores que cero, pero menores a cualquier número definido. Geométricamente podemos decir que los fractales están en algún punto entre el ser y el no ser, entre el cero y cualquier número racional.
Evidentemente esto es imposible en la física real, no sólo porque no es posible crear materia de la nada -de acuerdo al principio fundamental de la conservación de la materia y la energía-, sino porque es imposible dividir un objeto hasta convertirlo en puntos sin dimensión. No sólo habría que romper la esfera más allá de sus átomos y partículas subatómicas, sino dejar puntos infinitamente pequeños sin dimensión alguna. Pero la historia de la física –el descubrimiento del átomo, las partículas subatómicas y una infinidad de nuevas partículas que se descubren continuamente– nos demuestra que no hay una última partícula más allá de la cual no exista nada.
Un punto es una abstracción mental que omite -por conveniencia práctica- las contradicciones concretas. La descomposición geométrica de la realidad en figuras, cuerpos y números es indispensable para el entendimiento científico, pero es necesario reconocer sus límites. La paradoja muestra, entre otras cosas, los límites de la abstracción matemática. Las matemáticas no son sino una herramienta para comprender y transformar el mundo, nos ayudan a extraer las relaciones cuantitativas y mediciones del mundo material. Pero toda abstracción o nos ayuda a entender la realidad o también nos puede alejar de ella y volar al mundo de las abstracciones sin brújula ni ancla. Lo que decide entre la vinculación de las matemáticas y los teoremas con la realidad es la práctica humana y la transformación del mundo que corrobora o no teoremas e hipótesis.
Si bien es cierto que es imposible obtener dos esferas a partir de una -o romper un dólar para reensamblar millones-, la paradoja sí muestra -desde nuestro punto de vista- las propiedades dialécticas del infinito y su utilidad en las matemáticas. Por ejemplo: el cálculo -que opera con cantidades infinitamente pequeñas y un límite infinitamente grande en relación a ellas- implica la noción de infinito. Y es un poderoso instrumento que permite mediciones muy precisas que no serían posible de otra forma. A pesar de la oposición de mentes como Berkeley, que se opusieron al cálculo de Newton y Leibniz, fue el hecho de que funcionaba en la práctica lo que decidió el debate.
Bien es cierto que la paradoja de Banach –Tarski es más un ejercicio intelectual, muestra las paradojas que implica la noción de infinito y que parecen implícitas a éste–. Ya Engels había señalado que era en sí mismo una contradicción que el infinito se compusiera de la suma de “honradas finitudes”. Algo similar ocurre con la esfera que es finita e infinita desde diferentes ángulos. Es decir, la esfera es finita desde un punto de vista sintético –como una entidad definida entre otras– pero es infinita desde el punto de vista analítico –es decir, se puede dividir en partes más pequeñas infinitamente– y esto es así porque todo cuerpo no es sino un conjunto dentro de un universo infinito, todo ser no es más que un conjunto que contiene infinitos conjuntos en un universo infinito. La síntesis que hacemos los seres humanos para diferenciar los objetos y entenderlos, no excluye a dichos objetos de la interconexión universal y de formar parte de un todo. Sin embargo, este infinito se conoce a través de una progresión en sí misma infinita, no se puede conocer de golpe –como sucede en la intuición mística o en la revelación religiosa–. No es posible decir: aquí está el infinito completo, te lo presento y te lo revelo.
En conclusión. Si bien es imposible desarmar un guisante para rearmar el sol, no es menos cierto que el guisante contiene en sí mismo un universo infinito e inagotable. Todo objeto es, de cierta manera, un fractal del universo.

