La dialéctica de los números primos

“Como los números primos gemelos, estaban cerca, pero no lo suficiente para encontrarse realmente” Paolo Giordano, La soledad de los números primos

Escrito por David García Colín Carrillo

Los números primos – aquéllos que sólo son divisibles por sí mismos y la unidad- son los componentes básicos de todos los números enteros, ya que cualquiera de estos es resultado de la multiplicación de números primos. Todos los números -excepto los primos que son primordiales (de allí su nombre)- pueden descomponerse en una combinación de factores primos, siendo los números primos los átomos que componen a todos los demás -llamados números compuestos- en una combinación específica y única de esos “ladrillos” matemáticos. Esto nos dice el teorema fundamental de la aritmética.

Marx, en sus escritos matemáticos, ya había señalado el carácter dialéctico de los números en general y de los números primos en particular:

“El número es la determinación cuantitativa más pura que conocemos. Pero está completamente lleno de diferencias cualitativas. Cada número entero es, por un lado, una simple suma de unidades, pero al mismo tiempo posee propiedades particulares que no se derivan meramente de la suma, sino de la forma de la relación entre sus factores. Así, el número 6 no es solo la suma de seis unos, sino también el producto de 2 y 3, lo que le confiere propiedades diferentes de las de un número primo. El número, en su desarrollo, revela cómo lo cuantitativo se convierte en cualitativo, y cómo nuevas determinaciones surgen dentro de la simple adición de unidades. En esto se muestra la dialéctica inmanente del número mismo. ”

Además de lo anterior, los números primos muestran asombrosas relaciones dialécticas entre aleatoriedad y necesidad, azar y estadística y patrones que subyacen a lo aparentemente accidental. Trataremos de mostrar estas relaciones dialécticas increíbles.

Infinitos y aleatorios

Ya los antiguos pitagóricos llaman a los primos “indivisibles”, aquello que no puede dividirse sin perder su esencia. Dado que es imposible saber cuándo y dónde aparecerá un número primo, Eratóstenes ideó un procedimiento -la criba de Eratóstenes- para filtrar todos los números primos anteriores a un número dado: en una lista de números se van tachando todos aquéllos que son divisibles por otro número -los que son compuestos- y sólo nos quedan los primos.

Los números primos aparecen en la recta de números naturales de forma aparentemente accidental, pueden estar separados por una cifra -los primos gemelos- pueden estar separados por decenas, cientos, millones de números; la densidad de los números primos es inversamente proporcional a los dígitos que los componen, mientras más grandes son más solos están y su brecha puede ser incluso infinita -aunque nunca exista un último número primo-. Esto, por cierto, muestra ya la existencia de infinitos mayores y menores. Los únicos números primos que aparecen juntos son el 2 y el 3, siendo el primero el único primo par que existe. Incluso los poetas y escritores han elucubrado sobre “la soledad de los números primos” como una metáfora de amantes que están destinados a no encontrarse jamás después de haber estado juntos una única vez.

Euclides -por la misma época de Eratóstenes- demostró que los números primos son infinitos y lo hizo de una forma genial y sencilla -las ideas geniales suelen ser sencillas-. Esto lo hizo mediante una demostración con reducción al absurdo: supuso que el número de primos era finito, entonces cuando los multiplicas y sumas +1 tendrás un nuevo número que es o primo (contradiciendo que multiplicamos todos los primos) o que es divisible por primos (contradiciendo pues, por construcción, el nuevo número no puede ser divisible por ningún primo de la lista finita supuesta originalmente). Por cierto, este sencillo razonamiento demuestra la característica dialéctica del conocimiento humano: que es posible conocer características del infinito aunque sea imposible, por definición, agotarlo totalmente.

Euclides demostró que los números primos son infinitos pero no cuáles son, ni dónde se encuentran. De hecho, la naturaleza exacta de su distribución es uno de los grandes enigmas pendientes de las matemáticas modernas. Sabemos que los números primos son infinitos, pero no sabemos exactamente dónde aparecerán, parecen surgir como dardos tirados al azar sobre la recta de los naturales. Sin embargo, ocultan una regularidad estadística bastante precisa. Como decía Heráclito: a la verdad le gusta ocultarse.

Determinación estadística del azar

El famoso matemático alemán Carl Fredrich Gauss, con tan sólo 15 años de edad, demostró en 1792, que existe una regularidad estadística en la cantidad de números primos que anteceden a cualquier número natural, igual al número dado entre su logaritmo natural. Esto nos da una idea bastante aproximada -con un rango de error pequeño- de la cantidad de números primos que contiene un intervalo dado. Y de hecho esta regularidad estadística se ha precisado mucho más con fórmulas más modernas. O sea que, aunque los números primos parecen comportarse de forma aleatoria, su comportamiento obedece a una ley estadística. Azar y necesidad aparecen dialécticamente unidos, ya Demócrito había afirmado: “Todo sucede por el azar y la necesidad”. Además, los números primos se hacen más raros a medida que avanzamos en la recta numérica, los saltos entre ellos se hacen cada vez más largos, por lo que encontrar primos muy grandes es cada vez más difícil, y sin embargo son infinitos. Hasta 2024 el número primo más grande escrito en base 10 consta de 41 millones de dígitos.

Incluso con la fórmula de Gauss era imposible saber exactamente dónde aparecerá un número primo. Pero un alumno de Gauss, Bernard Riemann, obsesionado con los números primos hizo un descubrimiento revolucionario. Que la distribución de los ceros relevantes en una función de números complejos (llamada “función Z”) estaba relacionada con la distribución de los números primos, codificando su aparición. En esta función en la recta compleja -ya que se compone de número reales e imaginarios- aparece una gráfica en forma de montañas (puntos altos) y valles (puntos bajos), cada valle sobre el eje de las x representa los ceros, cuya aparición codifica la presencia de los números primos.

Esta es la famosa hipótesis de Riemann, enunciada en 1859, uno de los 7 grandes enigmas de las matemáticas, la pregunta del millón (literalmente, dado que existe una recompensa de un millón de dólares para quien pruebe o refute dicha hipótesis). Más de 150 años después de ser enunciada aún no ha sido demostrada. La hipótesis de Riemann parece ser cierta, al menos se ha probado para los primeros diez trillones de ceros no triviales de la función. De ser cierta esta hipótesis, se mostraría que debajo de su aleatoria aparición existiría la necesidad más férrea, y -a la inversa- la necesidad más férrea se manifiesta como aleatoriedad pura: el orden de caos.

El matemático Don Zagier expresó esta relación dialéctica entre azar y necesidad de la siguiente forma: “[…] los números primos crecen como malas hierbas entre los números naturales, y no parecen obedecer ninguna otra ley que la del azar, y nadie puede predecir dónde brotará el siguiente. El segundo hecho es aún más asombroso, ya que dice justo lo contrario: que los números primos muestran una regularidad pasmosa, que hay leyes que gobiernan su comportamiento, y que obedecen estas leyes con precisión casi militar.”

Patrones subyacentes

Sea como fuere, es indudable que en la distribución de los números primos aparecen patrones y regularidades locales muy llamativas que muestran un orden subyacente. En 1963 el matemático polaco Stanisław Marcin Ulam, aburrido en una conferencia científica, se puso a garabatear en su cuaderno una espiral compuesta por números naturales, en la que remarcó los números primos, revelando una regularidad sorprendente: los primos surgían como rayos que marcaban en diagonales ciertas partes de la espiral. El patrón se volvía más evidente con una espiral de 100 mil números y más aún con otra de 10 millones de cifras. Parecía ser como la sombra de la hipótesos de Riemann.

Además, aunque nunca se juntan, los números primos guardan cierta relación entre sí. En 2016 los científicos Kannan Soundararajan y Robert Lemke Oliver descubrieron que existe una relación entre el último dígito de un número primo y la probabilidad de que el siguiente número primo termine con determinados números, así, por ejemplo, si el número primo termina en 1 la probabilidad de que el siguiente comience con 3 es del 30%, con 7 otro 30%, con 9 un 22% y con 1 un 18%.

Un patrón quizá más sorprendente surge cuando se representan los números primos en una gráfica que multiplique a una función polinómica con Pi radianes. En la espiral así representada surgen patrones, concentraciones de números primos, que varían de acuerdo a la escala observada. Ambas gráficas -la de Ulam y la modular- muestran estructuras de números primos que parecen obedecer a un orden subyacente. Nuevamente parece ser la sombra gráfica de ls hipótesis de Riemann. Existen otras gráficas -con otras funciones similares- que muestran más patrones.

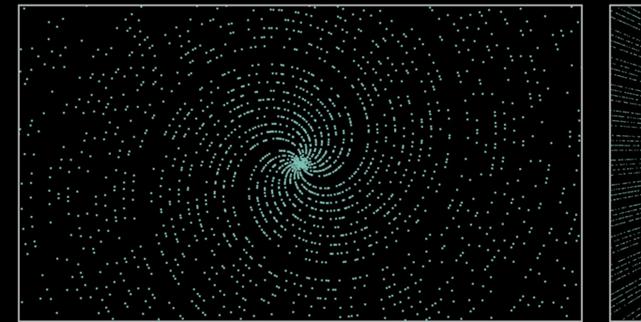
Hay estudios que muestran regularidad a niveles locales, las propiedades aritméticas de los números primos, su relación con polinomios, su concentración en ciertos puntos, etcétera. Pero no se ha descubierto si existe una ley general que una todos esos patrones a diversa escala, si existe alguna periodicidad o no. Algunas regularidades se dan a ciertas escalas para desparecer en otras.

Átomos matemáticos y átomos físicos

Es fácil saber el producto de número primos dados, pero la operación inversa -la factorización-es muy difícil de descifrar, sobre todo para números muy grandes. Debido a esto, los números primos se usan para encriptar datos personales e información financiera -como los datos de las tarjetas de crédito-. Cualquier cifra grande puede encriptarse en sus números primos que la componen. Engels -retomando los escritos de Marx sobre matemáticas- había reflexionado acerca de esta propiedad: “[…] los números primos comunican nuevas cualidades, determinadas en forma definitiva, a los números derivados de ellos por multiplicación” .

Ideas apocalípticas acompañan a los números primos tanto como a los fines de ciclo de los mayas. Artículos y youtubers sedientos de monentizar nos alertan sobre que la eventual demostración de la hipótesis de Riemann podría colapsar al sistema financiero mundial al revelar los códigos de encriptación y datos personales. Como si los números primos fuera fetiches y no herramientas que pueden mejorarse o sustituirse para fines humanos. Pero afortunadamente el principal enemigo del sistema financiero capitalista no es la distribución de los números primos, sino sus crisis y contradicciones inevitables. De cualquier forma, la mayoría de matemáticos opina que la hipótesis de Riemann es cierta y aún así sigue siendo extremadamente difícil factorizar en números primos a los grandes números.

Afortunadamente la utilidad de los números primos va mucho más allá de la vulgar y mezquina tarea de proteger al sistema capitalista, parece que su distribución nos dice una profunda verdad no sólo sobre la teoría de números sino sobre la naturaleza material: La distribución conocida de los ceros de la función z -que ya hemos dicho están relacionados con la distribución de los números primos- se parece mucho a la forma en que se comporta la energía a nivel subatómico en cieros sistémas cuánticos caóticos. Este hecho asombroso fue descubierto por los científicos Freeman Dayson y Hugh Montgomery en 1972, cuando ambos compararon gráficas que aparentemente no guardaban relación alguna: la distribución matemática de los ceros de la función z y los estados de cuánticos de los átomos .

Es como si la distribución de los ceros en la función z y la distribución de los números primos, de una parte, guardaran una relación con, por otra parte, los estados de energía de los átomos que componen la materia. Así, los átomos matemáticos -los números primos- y los átomos físicos tendrían una relación intrínseca. Esto es asombroso y muestra, de alguna manera, lo que había señalado Engels: que el pensamiento y la realidad no pueden, en última inatancia, contradecirse, pues el pensamiento es, en última instancia, un reflejo de la realidad material: “El hecho de que nuestro pensamiento subjetivo y el mundo objetivo se encuentren sometidos a las mismas leyes, y por lo tanto, además, que en último análisis no pueden contradecirse en sus resultados, sino que deben coincidir, gobierna por absoluto todo nuestro pensamiento teórico” .

Como materialistas dialécticos sabemos que esa correspondencia no es mecánica y está llena de contradicciones y retrocesos, pero el hecho de que ambas estructuras -la matemática y la atómica- confluyan por vías aparentemente sin relación alguna es una de las demostraciones más increíbles de la hipótesis materialista de Engels. El conocimiento de la realidad muestra vinculaciones asombrosas, que, a su vez, muestran la conexión universal de los fenómenos en el universo.

¿Podrá alguna vez demostrarse o refutarse la hipótesis de Riemann? La experiencia histórica nos dice que lo que no sabemos ahora lo sabremos mañana. También que el infinto se demuestra en una sucesión infinita de descubrimientos humanos finitos. Hasta ahora, y para números muy grandes, la hipótesis de Riemann parece cierta, podría decirse que para afectos prácticos lo es. ¿Pero se podrá descubrir la ley subyacente que determina esa propiedad? No sabemos sin esa distribución se mantiene constante, o si en determinado punto es negada o suparada por otro tipo de distribución diferente. No sabemos si estamos mirando la escala adecuada para decidir esa cuestión. No sabemos si ese patrón es reductible a una sola ley matemática que pueda formularse simplemente o debemos conformarnos con asumir su validez relativa simplemente porque a efectos prácticos parece cierta. El infinito revela sus secretos en una sucesión infinita, pero se guarda otros sin que sea posible agotarlos nunca -por eso es infinito-. No sabemos si intentar demostrar dicha hipótesis sea tan necio como intentar encontrar el número natural más grande o, por el contrario, el secreto esté esperando a la vuelta de la esquina. Lo que es seguro es que el camino nos prepara descubrimientos sin fin. ¿Al fin y al cabo no es ésta la experiencia misma del conocimiento?