Dialéctica de los números imaginarios
David Rodrigo García Colín Carrillo
La historia de las matemáticas -como del conjunto del conocimiento científico- está marcado por resistencias a las ideas revolucionarias, ideas que irrumpen como bichos raros que, a pesar del rechazo y repulsión inicial que generan, se demuestran en la práctica como fundamentales para el avance del conocimiento humano, revolucionando el conocimiento científico. La lenta introducción del cero en occidente desde oriente, el necio secretismo de los pitagóricos con respecto a los números irracionales (números que no se pueden expresar como una fracción exacta de dos números enteros, tales como π o e) -que parecían mostrar que su dios “número” se había vuelto loco e incluso se dice que arrojaron al mar a quien reveló su existencia- o la resistencia para aceptar las contradicciones propias del infinito y estructuras paradójicas como los fractales son muestra de ello.
Otro caso muy interesante es la introducción de los números imaginarios y complejos (aquellos que al elevarse al cuadrado resultan en un número negativo). Por su origen las matemáticas estaban muy atadas a la geometría convencional que servía simplemente para medir áreas, volúmenes y pesos la existencia de raíces negativas parece un completo sinsentido.
Geométricamente es muy claro que x3 es un cubo con lados de longitud x Pero x-3no se puede representar en la geometría normal ¿Cómo podría visualizarse un cubo cuyos lados midieran -3? Es una paradoja. Además, todo número multiplicado por sí mismo -ya sea positivo o negativo- da siempre positivo ¿Cómo puede tolerarse, entonces, la raíz de un número negativo? Esto desafía es sentido común y la razón convencional. Y sin embargo es necesario aceptar esos números si quiere resolverse ecuaciones tan elementales como x2 = 0 que no tienen solución en los números reales.
Los números imaginarios surgen como contrapartida de los números reales en un cierto grado de desarrollo de las matemáticas, son su “fantasma” dialéctico, su “ser otro”. Proyectados en el plano surge se plasma la dualidad de los números complejos, con su parte real e imaginaria, y esta dialéctica expresa de mejor manera las profundidades físicas de la naturaleza. Esto lo trataremos de mostrar en el presente artículo.
El ascenso de un bicho raro
De Herón de Alejandría data el registro más antiguo -año 50 D.C- de una raíz negativa resultado de hacer cálculos sobre secciones de pirámides. El famoso Al Juarismi -en la edad media musulmana- presentó raíces positivas y negativas como resultado de ecuaciones de segundo grado. En el año 850 el matemático indú Mahavira afirmó: “como en la naturaleza de las cosas un negativo no es un cuadrado, por tanto, no puede tener raíz cuadrada”. Ya las antiguas civilizaciones en Egipto, Babilonia, Grecia, China, India y en Persia se habían topado con ecuaciones de tercer grado a las que no encontraron solución -precisamente porque algunas de ellas llevaban a resultados con raíces negativas-. Incluso Luca Paccioli -el maestro de matemáticas de Leonardo Davinci- sostuvo en su “Summa de artimética” que las ecuaciones cúbicas eran imposibles de solucionar[1].
Como vemos, las raíces negativas aparecían como fantasmas de ciertos problemas matemáticos. Aunque surgía de operar con los números reales, la raíz negativa parece un “antinúmero” que no tiene solución ni representación en la recta de los números reales -ya que ningún número, sea positivo o negativo, multiplicado por sí mismo da negativo-. ¿Cómo podían los números reales dar lugar a esos “antinúmeros”?. Y a la inversa, números imaginarios elevados al cuadrado pueden dar lugar a números reales negativos (por ejemplo: i2 = -1 ), es como si el número y su “fantasma” estuvieran mutuamente implicados. El matemático Suizo, contemporáneo de Leibinz, Johan Bernoulli calificó a los números imaginarios como “un anfibio entre el ser y la nada”. Hegel los relacionó con el ser y la nada: “El número imaginario es una determinación cuantitativa que deja de ser una mera magnitud empírica y se convierte en una determinación de la reflexión; una magnitud que es y no es a la vez, que se mantiene sólo en su contradicción.[2]”
No fue sino hasta el renacimiento italiano en donde encontramos los comienzos del camino que nos lleva a los números complejos. Fue en un “duelo matemático” donde surgieron como solución. En esos días los matemáticos solían retarse con problemas cuya solución dotaba de prestigio y puestos a intelectuales que luchaban por el mecenazgo y la sobrevivencia. En 1535 el matemático autodidacta veneciano Niccolo Fontana -apodado Tartaglia por ser tartamudo- difundió el rumor de que podía resolver ecuaciones de tercer grado por lo que fue retado a un duelo de 30 problemas matemáticos, que pudo resolver en unas cuantas horas mientras que su contrincante no pudo resolver ninguno. El portentoso triunfo de Tartaglia llegó a oídos de Gerolamo Cardano, un hombre del renacimiento que además de médico era filósofo, matemático, físico, químico y muchas cosas más; fue un perseguido de la inquisición por sus ideas religiosas poco ortodoxas. Rogó a Tartaglia que le revelara el método de la solución de la cúbica reducida hasta que, entre maldiciones y ruegos, Tartaglia le reveló el secreto a Cardano a cambio de recomendarlo a poderosos mecenas, haciendo jurar a Cardano que no revelaría nunca el secreto. Afortunadamente Cardano no cumplió su promesa -ya que se había enterado que otro matemático -Scipione dal Ferro- había descubierto el método antes) publicando el método en su obra Arts Magna en 1545. Sin embargo, el propio Cardano consideró las raíces negativas como un artilugio tan sutil como inútil.
Inspirado en el trabajo de Cardano el matemático Rafael Bombelli pudo perfeccionar el método para resolver no sólo lacúbica reducida sino cualquier ecuación de tercer grado utilizando ya sin tapujo alguno las raíces negativas y afirmando que éstas eran un nuevo tipo de número. Pero la obra de Bombelli pasó casi desapercibida y matemáticos importantes de su tiempo -como Simon Stevin- consideraron que no tenía sentido “perder el tiempo en inexactitudes”.
Pero le verdad es necia, poco a poco, la práctica matemática mostró que para trabajar con polinomio de grado n los números imaginarios no sólo eran útiles sino que vagamente se comenzaba a mostrar que tenían que ver con algo fundamental en el álgebra. Engels escribió: “Para el buen sentido parece un absurdo resolver una magnitud definida, por ejemplo una expresión binominal, en una serie infinita, es decir, en algo indefinido. ¿Pero dónde estaríamos sin serie infinitas y sin el teorema del binomio?”[3].
Descartes utilizó frecuentemente estos números y los popularizó con el nombre de números imaginarios- mostrando su desconfianza con estos bichos raros-. A una carta de Cristian Huygens al gran filósofo Leibniz -quien tuvo correspondencia con las mentes más grandes de su tiempo- Huygens afirma: “Lo que me escribes sobre cantidades imaginarias que, no obstante, cuando son sumadas dan una cantidad real, me es sorprendente y totalmente nuevo. Uno nunca creería que esto es cierto y debe haber algo escondido en ello que es incomprensible para mí”[4]. Con su gran genio e intuición Leibniz estaba decidido a demostrar que las fórmulas de Cardano eran válidas para toda ecuación cúbica y utilizó los números imaginarios, sin ninguna vergüenza ni pudor, para resolver integrales.
Ambos, Leibniz y Bernoulli, entablaron un debate sobre la naturaleza de los logaritmos negativos. Mismo debate que fue resuelto por Euler, quien introdujo el símbolo “i”, al combinarse con los números reales dieron como resultados los números complejos. Friedrich Gauss profundizó en su representación geométrica en el plano complejo, dando como fruto el teorema fundamental del álgebra que establece que toda ecuación polinómica de grado n tiene n soluciones en el conjunto de los números complejos. Pero el propio Gauss dudó en publicarlo debido a sus reservas sobre la naturaleza metafísica de los números complejos. Sin embargo, este teorema nos permite resolver ecuaciones que no tendrían solución de otra manera.
Gauss encontró la solución a sus reservas metafísicas en la representación grafica -el plano complejo- de dichos números, mostrando que no eran realmente imaginarios, sino que tenían una expresión un eje perpendicular al eje de los números reales, como si al eje de los números reales se le agregara una dimensión adicional. Los números complejos son en sí mismos una contradicción dialéctica compuesta por una parte “real” y otra “imaginaria” que resultan en una representación más profunda e interesante de la materia.
Engels hizo una interesante reflexión sobre los números negativos que puede también aplicarse a los imaginarios: “Las magnitudes negativas del álgebra son reales sólo en la medida en que tienen vinculación con magnitudes positivas, y sólo dentro de esa relación con éstas. Fuera de dicha vinculación, tomadas en sí mismas son puramente imaginarias. En trigonometría y geometría analítica, junto con las ramas de las matemáticas superiores de las cuales éstas son la base, expresan una dirección definida del movimiento, opuesta a la dirección positiva. […].[5]” Esta reflexión de Engels resulta relevante en la relación entre los números reales e imaginarios, que juntos representan en el plano compelo, un tipo de movimiento que no puede representarse de otra forma. De pasada, Marx -quien estaba particularmente interesado en temas matemáticos- hace en El Capital una observación similar: “[…] un objeto puede tener precio sin tener valor. En tal caso, el precio es imaginario, como ciertas magnitudes en matemáticas”[6]. O sea que, los números imaginarios no tienen representación tangible en la recta de los números reales, pero nacen de las relaciones necesarias entre los números que, a su vez, representan el movimiento real de la materia a un nivel más profundo, que escapa al sentido común.
¿Matemática pura?
La introducción de los números imaginarios emancipó al álgebra de la geometría, y convirtió al álgebra en un instrumento mucho más poderosos para solucionar problemas que eran aparentemente imposibles de resolver. Parecía que las matemáticas se alejaban de la realidad que le había dado origen -contar, pesar, medir volúmenes, pesos, áreas- para fugarse a un mundo imaginario. Sin embargo, paradójicamente, demostraron ser una herramienta muy poderosa para comprender de manera más profunda esa realidad. Engels ya había señalado la relación entre las magnitudes aparentemente imaginarias y la realidad materia: “De entre todos los progresos teóricos, no cabe duda de que ninguno se encuentra a tan gran altura, como triunfo de la mente humana, como el descubrimiento del cálculo infinitesimal en la última mitad del siglo XVII. Si existe algún hazaña pura y exclusiva de la inteligencia humana, debemos encontrarla aquí. El misterio que todavía hoy rodea a las magnitudes empleadas en el cálculo infinitesimal, las diferencias e infinitos de distintos grados, es la mejor prueba de que aún se continúa imaginando que lo que se encara aquí son puras creaciones e imaginaciones libres de la mente humana, y que en el mundo objetivo no existe nada correspondiente. Sin embargo, ocurre todo lo contrario, La naturaleza ofrece prototipos de todas esas magnitudes imaginarias”[7]. A continuación, Engels proporciona ejemplos de la gravedad terrestre con respecto a cuerpos simples y lo infinitamente pequeño con relación a cuerpos de la vida cotidiana, a la lenta evaporación de moléculas, etc.
Pero ¿dónde se encuentra el “prototipo” natural de los números imaginarios? Después de todo, si tienen en una amplia gama de aplicaciones en la física es porque deben reflejar correctamente dichos procesos. Si fueran sólo inventos como los unicornios o duendes no tendrían más aplicación que en los cuentos infantiles. Veremos que el correlato real de los números complejos -y por ende los números imaginarios- se encuentra en procesos que implican ondas, oscilaciones, rotaciones, fases y frecuencias, o sea un tipo especial de movimiento que requiere vectores para su representación.
La espiral dialéctica en el plano complejo
Inicialmente se creía que los números imaginarios eran sólo un paso intermedio para resolver ecuaciones cuadráticas, una especie de comodín, que se anulaba antes de obtener la solución. El que Descartes los haya llamado “imaginarios” expresa la desconfianza que generaba su uso. Sin embargo, con la introducción de los números imaginarios en la ecuación de Schrödinger -que describe el movimiento undulatorio de las partículas subatómicas- los números imaginarios se convirtieron en elementos esenciales para representar lo que sabemos del átomo. El propio Schrödinder se mostró incómodo de que los números imaginarios estuvieran implicados en una representación real del funcionamiento físico de la materia: “Lo incómodo aquí, y de hecho algo que debe ser objetado, es el uso de números complejos, la función de onda es fundamentalmente una función real”[8].
Pero lejos de ser objetado el uso de estos números ha sido confirmado en este plano y otros, quizás porque introduce una dimensión perpendicular a la línea de los números reales, lo que dota de una profundidad mayor al plano complejo que, de alguna manera, capta algo profundo de la realidad que se nos escapa de otra manera.
Al multiplicar por i rotamos 90 grados en el plano complejo, lo que resulta en un círculo cerrado si continuamos con la operación. Pero con la ecuación eix el círculo se convierte en una espiral que asciende por el eje x. Esta espiral en el plano complejo representa dos caras de la realidad: una que podemos ver -expresada en la parte real de la ecuación- que se dibuja en el plano como una cosenoidal, y la parte imaginaria que se representa como una onda senoidal; ambas -en unión dialéctica- nos dan una representación espiral más exacta de fenómenos dinámicos que implican oscilaciones, rotaciones y fases; tales como el movimiento de la partículas subatómicas -cuya onda expresa la probabilidad de encontrar una partícula y su estado- las ondas de luz o de radio; en la ingeniería los números complejos se usan para producir circuitos, medir señales; aparecen también en la representación matemática de los fractales, etcétera. Y así como, a decir de Engels, “El cálculo diferencial permite que las ciencias naturales representen, por primera vez, en forma matemática, procesos y no solo estados: movimiento”[9], el plano complejo hace lo mismo con otros tipos de movimiento.
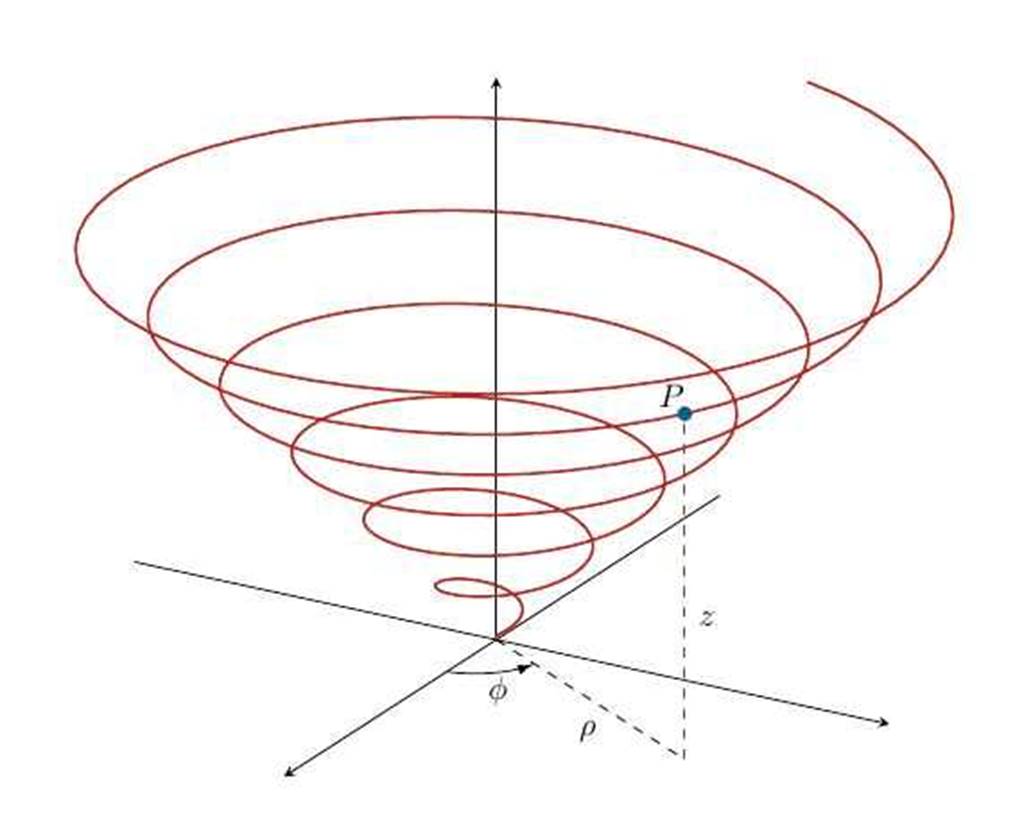
El físico Freeman Dyson escribió: “Resulta que la ecuación de Shödinger describe correctamente todo lo que sabemos del comportamiento de los átomos. Es la base de toda la química y mucha de la física. Y esa raíz cuadrada de -1 implica que la naturaleza trabaja con números complejos y no con reales. Este descubrimiento fue una total sorpresa para Schödinger y para todo el mundo”[10]. Resulta que el movimiento en es espiral -implícito en el plano complejo- revela una realidad mucho más profunda que la geometría tradicional que huía como de la peste de las raíces de números negativos.
Terminemos con una reflexión de Engels: “Como todas las demás ciencias, la matemática ha nacido de las necesidades de los hombres. […]. Al llegar a cierto punto de evolución se separan del mundo real las leyes abstraídas del mismo, se le contraponen como algo independiente, como leyes que llegaran desde fuera y según las cuales tiene que disponerse el mundo. […]. Y así se aplica la matemática pura, aunque ha sido tomada sencillamente de se mundo y no representa más que una parte de las formas de conexión del mismo, única razón por la cual es aplicable”.[11]
[1] https://www.youtube.com/watch?v=VN7nipynE0c
[2] Hegel, Ciencia de la lógica, Libro I, Argentina, Solar, p. 119.
[3] Engels, Dialéctica de la naturaleza, p. 210.
[4] https://www.youtube.com/watch?v=lyQaST9IX0I&t=635s
[5] Engels, Dialéctica de la naturaleza, pp. 210-211.
[6] Marx, El Capital, Tomo I, cap. III, sección 1: “Medida de los valores”.
[7] Engels, Dialéctica de la naturaleza, pp. 212-213.
[8] https://www.youtube.com/watch?v=VN7nipynE0c
[9] Engels, Dialéctica de la naturaleza, p 216.
[10] https://www.youtube.com/watch?v=VN7nipynE0c
[11] Engels, Antidühring, pp. 25-26.